Robust Principal Component Analysis
Principal Component Analysis is a very commonly used dimensionality reduction technique that finds a low rank representation of data. Classical PCA is highly sensitive to Outliers. A method to handle outliers and corrupted data is the Robust PCA.
Robust Principal Component Analysis
Problem Formulation
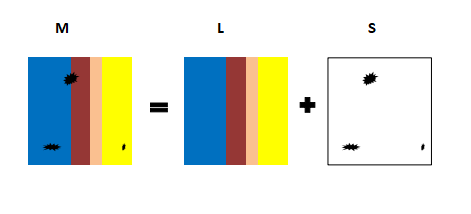
where M is the data matrix, L is the low rank representation to be estimated. S is the sparse matrix (Outliers).
L and S can be obtained by solving the optimization problem: \(\underset{L,S}{\operatorname{argmin}} rank(L) + \lambda \left \lVert S \right \rVert_{0} \text{ subject to : } M=L + S\)
This problem is intractable so we apply convex relaxation: \(rank(L) \longrightarrow \left \lVert L \right \rVert_{*}\) (Nuclear norm) and \(\left \lVert S \right \rVert_{0} \longrightarrow \left \lVert S \right \rVert_{1}\)
\[rank(L) = \# \{ \sigma(L) \neq 0\} \longrightarrow \left \lVert L \right \rVert_{*}= \sum_{i} \sigma(L)\] \[\left \lVert S \right \rVert_{0} = \# \{ \S_{ij} \neq 0\} \longrightarrow \left \lVert S \right \rVert_{1}= \sum_{i,j} \lvert S_{ij} \rvert\]The optimization problem simplifies to: \(min \ \lVert L \rVert_* + \lambda \lVert S \rVert_1 \text{ sub to: } M= L+S\)
Alternating direction method of multipliers
\(\newcommand{\Lagr}{\mathcal{L}}\)
The augmented Lagrangian of the optimization problem is:
ADMM updates:
\[L_{k+1} =\underset{L}{\operatorname{\text{arg max}}} \left \{ \ \lVert L \rVert_* + \dfrac{\rho}{2} \ \Big\lVert M - L-S_{k} + \frac{Y_k}{\rho} \Big\rVert_F^2 \ \right \}\] \[\boxed{ \implies L_{k+1} =D_{1/\rho} \left(M - S_k + \frac{Y_k}{\rho} \right) }\] \[S_{k+1} =\underset{S}{\operatorname{\text{arg max}}} \left \{ \ \lambda \lVert S \rVert_1 + \dfrac{\rho}{2} \ \Big\lVert M - L_{k+1}-S + \frac{Y_k}{\rho} \Big\rVert_F^2 \right \}\] \[\boxed{ \implies S_{k+1} =S_{\lambda/\rho} \left(M - L_{k+1} + \frac{Y_k}{\rho} \right) }\] \[\boxed{ \implies Y_{k+1} = Y_k + \rho \ (M-L_{k+1}-S_{k+1}) }\]\(D_{1/\rho}\) is the singular value thresholding operator defined as: \(D_{1/\rho}(X) =U \ D_{1/\rho}(\Sigma) V \ ; \ D_{1/\rho}(\Sigma) = diag\{(\sigma_i - 1/\rho)_+ \}\)
\(S_{\lambda/\rho}(x)\) is the soft thresholding operator defined as: \(S_{\lambda/\rho}(x) = sgn(x) \ max\left( |x|- \lambda/\rho ,0\right )\)
Implementation
| Input (M) | Output 1 (L) | Output 2 (S) |
|---|---|---|
 |
 |
 |
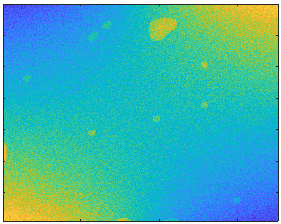 |
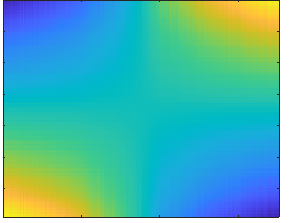 |
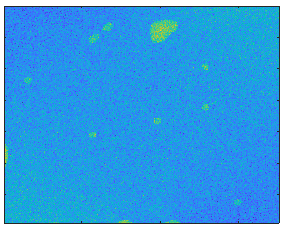 |
Applications
Face recognition, Anomaly detection, Image Denoising,Text mining, Video Surveillance
Github Link
References
- Emmanuel J Candès, Xiaodong Li, Yi Ma, and John Wright. Robust Principal Component Analysis? Journal of the ACM (JACM), 58(3):11, 2011.
- Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers
- John Wright, Arvind Ganesh, Shankar Rao, Yigang Peng, and Yi Ma. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization
