Recommendation Systems

Machine learning based personalized recommendation systems are used in a wide variety of applications such as electronic commerce, social networks, web search, Over the top media. Recommendation systems are personalized to a user based on his/her interests. This helps user narrow down option from a wide variety of content that is accesible to them. This projects explores some common matrix completion techniques that are based on Collaborative filtering.
Introduction
Recommendation Systems typically are made through one of two approaches - Collaborative Filtering and Content based filtering. Collaborative filtering makes recommendations based on recorded past interactions between users and items. It works on the principle that if a group of users share similar rating on a set of item, they would be likely to rate other items similarly. Content based filtering on the other hand uses a set of features to characterize an item and builds user profile based on his previous liking (For eg : User age, Genre)
Regularised Matrix Factorisation model
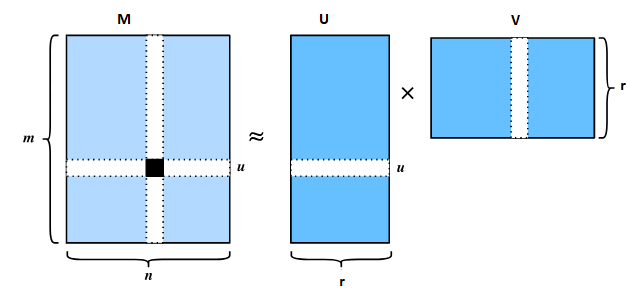
The matrix factorization model is a generalization of SVD decomposition to find a low rank matrix factorization approximation.
You are given a set of ratings (from one star to five stars) from users on many movies they have seen. Using this information, we have to develop a personalized rating predictor for a user on unseen movies. Typically the rating is between 1 and 5 (stars).
Data representation:
Suppose we have m users and n movies, and a rating given by a user on a movie they have seen. We can represent this information as a rating matrix M (size M x N). Rows of M represent users, while columns represent movies. Each cell of the matrix may contain a rating on a movie by a user. For example,\(M_{15,47}\) contains rating on the movie 47 by user 15. If he gave 4 stars, M15,47 = 4. It is almost impossible for everyone to watch large portion of movies in the market, this rating matrix should be very sparse in nature. Typically, only 1% of the cells in the rating matrix are observed in average. All other 99% are missing values, which means the corresponding user did not see the corresponding movie. Our rating predictor should estimate those missing values by learning the user’s preference from the available ratings.
Approach to modeling: Latent Factors
Our approach for this problem is matrix factorization. We assume that the rating matrix M is a low-rank matrix. Intuitively, this reflects that there is only a small number of factors (e.g, genre, director, actor, etc.) that determine like or dislike. Let us choose r number of factors. Then, we learn a user profile U (size M x r) and an item profile V (size N x r) (M and N are the number of users and films)
A rating for user u on movie i can be approximated by \(M_{u,i} = \sum_{k=1}^{r} U_{u,k} V_{i,k}\)
We want to minimize squared reconstruction error over the training data. To avoid overfitting, we aslo add L2 regularization terms to penalize for large values in U and V. The objective function becomes:
\[E(U,V) = \sum_{(i,j) \in M} (M_{i,j} - U_{i}^TV_{j})^2 + \lambda \sum_{i,k} U_{i,k}^2+ \lambda \sum_{j,k} V_{j,k}^2\]where \(U_{i}\) is the \(i^{th}\) row of U and \(V_{j}\) is the \(j^{th}\) row of V. \(\lambda\) is the hyperparameter controlling the degree of regularization.
Since, U and V are related there is no closed form solution. We can use gradient descent: \(U_{i,k} \rightarrow U_{i,k} - \mu \frac{\partial E(U,V)}{\partial U_{i,k}} \ ; \ V_{j,k} \rightarrow V_{j,k} - \mu \frac{\partial E(U,V)}{\partial V_{j,k}}\); \(\mu\) is the learning rate.
def my_recommender(rate_mat, lr, with_reg):
"""
:param rate_mat: Rating Matrix
:param lr: Number of Latent Factors
:param with_reg: boolean flag, set true for using regularization and false otherwise
:return: User profile U , Item Profile V
"""
# Tune hyperparameters according to your dataset
max_iter = 500
if(with_reg):
learning_rate = 2e-4
reg_coef = 0.9981
else:
learning_rate=0.0002
reg_coef=0
n_user, n_item = rate_mat.shape[0], rate_mat.shape[1]
err1=0
err2=0
U = np.random.rand(n_user, lr) / lr
V = np.random.rand(n_item, lr) / lr
Iter=0
Mask=rate_mat>0
while(Iter<max_iter):
Iter=Iter+1
U_new= U+ (2*learning_rate*(((rate_mat-U.dot(V.T))*Mask)@V))- (2*learning_rate*reg_coef*U)
V_new= V+ (2*learning_rate*(((rate_mat-U.dot(V.T))*Mask).T@U))-(2*learning_rate*reg_coef*V)
err1= np.sum(((U_new.dot(V_new.T) - rate_mat) * Mask) ** 2)
err2= np.sum(((U.dot(V.T) - rate_mat) * Mask) ** 2)
# Convergence criteria - Change in error between two iterations is very small
if(err2-err1<1e-3):
break
U=U_new
V=V_new
return U, V
Results: I applied this algorithm on simulated ratings dataset similar to Netflix (Avaialable in Github). These are the results:
| No of Latent factors (r) | Train RMSE | Test RMSE | Elapsed Run Time |
|---|---|---|---|
| 1 | 0.9175 | 0.9483 | 27.31 |
| 3 | 0.8640 | 0.9336 | 28.07 |
| 5 | 0.8388 | 0.9375 | 28.47 |
| 7 | 0.8188 | 0.9344 | 28.58 |
| 9 | 0.8048 | 0.9269 | 29.04 |
| 11 | 0.7979 | 0.9316 | 30.24 |
The RMSE on training set decreases with increasing lowRank. This result is expected because we are including more latent features to explain the data. However increasing K beyond a certain point will risk overfitting the data and lower accuracy on the test set.
SVD++ model:
The SVD++ model is one of the most accurate model in Netlix Prize. \(U_{i}^TV_{j}\) only captures the relationship between users and items . In the real world, the observed rating may be affected by user or item characteristic. For example, suppose one wants to predict the rating of the movie “Avengers” by the user “Adam”. Now, the average rating of all movies on one website is 3.5, and Adam tends to give a rating that is 0.3 lower than the average because he is a critic. The movie “Avengers” is better than the average movie, so it tends to be rated 0.2 above the average. Therefore, considering the user and movie bias information we can update the predictions to:
\[r_{ij}= \mu + b_i +b_j + U_{i}^TV_{j}\]where \(\mu\) is the average overall rating and \(b_u,b_i\) are the observed deviations for user i and movie j.
The SVD++ model aslo introduces the implicit feedback information based on SVD. It adds a factor vector \(y_j\)for each item, and these item factors are used to describe the characteristics of the item, regardless of whether it has been evaluated. Then, the user profile matrix U is modelled, so that a better user bias can be obtained. The predictive rating of the SVD++ model is:
\(r_{ij}= \mu + b_i +b_j + \big(U_{i}+ \lvert R(i)\rvert^{-\frac{1}{2}} \sum_{j \in R(i)} y_j \big)^TV_{j}\); \(\ R(i)\) is the number of items rated by user i.
Computational Algorithms for Matrix Completion
Matrix Completion Formulation:
Assuming the that the rating matrix X is low rank, the missing values can be imputed by solving the optimization problem:
\(min (rank(Z))\) subject to \(P_{\Omega}(X)=P_{\Omega}(Z)\) where \(P_{\Omega}\) is the projection function defined as \(P_{\Omega} \begin{cases} X_{i,j} & \text{ if (i,j) is observed}\\ 0 & \text{ if (i,j) is not observed} \end{cases}\)
This problem is intractable so we apply the convex relaxation. The relaxed problem takes the form: \(min(\lVert Z \rVert _{*})\) subject to \(P_{\Omega}(X)=P_{\Omega}(Z)\)
Singular Value Thresholding Algorithm:
For a fixed \(\tau>0\) and a sequence of \(\delta_k\) positive step sizes, start with \(Y_0= 0 \in ℝ^{n1 \times n2}\), iteratively compute (k is the iteration):
\[\begin{cases} Z^k=S_{\tau}(Y^{k-1})\\ Y^{k}= Y^{k-1}+ \delta_{k}P_{\Omega}(X-Z^k) \end{cases}\]Proximal Backward Forward Splitting Algorithm:
In real life data, to account for noisy obervation we relax the equality constraint. \(min(\lVert Z \rVert _{*})\) subject to \(\lVert P_{\Omega}(X)-P_{\Omega}(Z) \rVert _{F}^2 < \epsilon\).
The Lagrangian equivalent of the problem: \(min \{ \lambda \lVert Z \rVert _{*} + \frac{1}{2} \lVert P_{\Omega}(X)-P_{\Omega}(Z) \rVert _{F}^2 \}\).
This can be solved using PFBS algorithm: \(\begin{cases} Z^k=S_{\lambda \delta_{k-1}}(Y^{k-1})\\ Y^{k}= Z^k+ \delta_{k}P_{\Omega}(X-Z^k) \end{cases}\)
Github Link
References
- Wang S, Sun G, Li Y. SVD++ Recommendation Algorithm Based on Backtracking. Information. 2020; 11(7):369.
- Google Developers Machine Learning
- A. Ramlatchan, M. Yang, Q. Liu, M. Li, J. Wang and Y. Li, A survey of matrix completion methods for recommendation systems in Big Data Mining and Analytics, vol. 1, no. 4, pp. 308-323, December 2018
- Jian-feng Cai, Emmanuel J. Candes, And Zuowei Shen. A Singular Value Thresholding Algorithm For Matrix Completion
